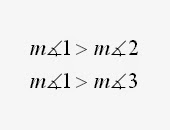INTRODUCTION

People around the world had been constantly improving the quality of education. Doing so will require the use of technology in the teaching and learning process. Technology had been a part of the educational system these past decades. As this improves, education also advances. Applying technology in the classroom will both involve the interaction between the students and the teacher. Using it will motivate the students to think and generate their own ideas and concepts. At the same time, it will also give them the opportunity to be computer literates and be in the trend when it comes to technology integration.

Mathematics is a branch of science that deals with numbers, operations, quantities, shapes and the relationships between them. This is an amazing subject, but most students consider this as a very difficult course to learn, others even avert themselves from getting involved in any situations requiring mathematical knowledge. This should not be. Unknowingly, mathematics is in fact a part of our daily lives; even just buying in stores, summing up your bill and counting your change. These simple acts manifest basic mathematical skills. We should all learn to love mathematics!

If we think about it, applying technology in teaching and learning mathematics is not that difficult, if we will be able to do it successfully, students and teachers will gain more knowledge from both of it.

We, the bloggers, had made this page in partial fulfillment of the course requirements in Educational Technology 1. This output manifests how we applied technology in teaching and learning mathematics. This will also be very helpful for our profession as future teachers. This page includes the grade 8 K-12 curriculum mathematics lessons which are Module 8: Triangle Inequalities and Module 9: Parallelism and Perpendicularity. This contains information about its definitions, theorems, postulates and some examples, figures and exercises including interactive videos and games. We hope that you find our work helpful in your mathematical learning.

PARALLELISM AND PERPENDICULARITY

Have you ever wondered how carpenters, architects and engineers design their work? What factors are being considered in making their designs? The use of parallelism and perpendicularity of lines in real life necessitates the establishment of these concepts deductively.

LEARNING GOALS AND TARGET

• The learner demonstrates understanding of the key concepts of parallel and perpendicular lines.
• The learner is able to communicate mathematical thinking with coherence and clarity in solving real-life problems involving parallelism and perpendicularity using appropriate and accurate representations.

PARALLELISM

Two lines are parallel if and only if they lie on the same plane (coplanar) and do not intersect (Figure 1).

Figure 1

Figure 2. m || n and t is a transversal line

From the figure above (figure 2), 

Transversal line - a line that intersects two or more lines at different points

Exterior Angles - angles made by a transversal that are outside the region between the two intersected lines

                    example : ∠1, ∠2, ∠7 and ∠8

Interior Angles - angles made by a transversal that lie inside the region between the two intersected lines

                    example : ∠3, ∠4, ∠5 and ∠6

Alternate-Exterior Angles - a pair of non-adjacent exterior angles on opposite sides of the transversal

                    example : ∠1 and ∠8, ∠2 and ∠7

Alternate-Interior Angles - a pair of non-adjacent interior angles on opposite sides of the transversal

                    example: ∠3 and ∠6, ∠4 and ∠5

Corresponding Angles - a pair of non-adjacent angles - one interior, one exterior - both on the same side of the transversal

                   example : ∠1 and ∠5, ∠3 and ∠7, ∠2 and ∠6, ∠4 and ∠8

Figure 3.

From the figure above (Figure 3)

1. ∠1 and ∠7 - alternate exterior angles
2. ∠3 and ∠5 - alternate interior angles
3. ∠4 and ∠8 - corresponding angles
4. ∠2 and ∠6 - corresponding angles
5. ∠4 and ∠6 - alternate interior angles
6. ∠2 and ∠8 - alternate exterior angles

If two lines are cut by a transversal, then the two lines are parallel if:

• corresponding angles are congruent.
• alternate-interior angles are congruent.
• alternate-exterior angles are congruent.
• interior angles on the same side of the transversal are supplementary.
• exterior angles on the same side of the transversal are supplementary.

You may visit the following sites to strengthen your knowledge regarding the different angles formed by parallel lines cut by a transversal line and how they are related with one another;

Properties of Parallel Lines (Part 1 of 2)

Properties of Parallel Lines (Part 2 of 2)

To enhance your knowledge, you may try to answer the question in the following link:

http://www.regentsprep.org/Regents/math/geometry/GP8/PracParallel.htm

 

Proving Lines are Parallel

The following theorems will lay down conditions which guarantee parallelism of two lines

• If 2 coplanar lines are both perpendicular to the same line, then they are parallel.
  
• CAP Theorem. If 2 lines have transversal and a pair of congruent Corresponding Angles, then the    lines are parallel.
  
• AIP Theorem. If 2 lines have a transversal and a pair of Alternate Interior Angles, then the lines are parallel.
  
• AEP Theorem. If 2 lines have a transversal and a pair of congruent Alternate Exterior angles, then the lines are parallel.
  
• If 2 lines have a transversal and interior angles on the same side of the transversal are supplementary, then the lines are parallel.
  
• If 2 lines are parallel to a third line, then they are parallel to each other. If a // b, and b //c, then a //c.
  

Criteria of parallelism of straight line and plane:

1)  If a straight line, lying out of plane, is parallel to some straight line, lying in the  

     plane, then it is parallel to this plane.

2)  If a straight line and a plane are perpendicular to the same straight line, then they  

     are parallel.

PERPENDICULARITY

Two lines that intersect to form right angles are said to be perpendicular. This is not  limited to lines only. Segments and rays can also be perpendicular. A perpendicular bisector of a segment is a line or a ray or another segment that is perpendicular to the segment and intersects the segment at its midpoint. The distance between two parallel lines is the perpendicular distance between one of the lines and any point on the other line.
Two lines are Perpendicular if they meet at a right angle (90°).

        

                                              

Line PY is a perpendicular bisector and XZ ⊥ PY

The distance between the two right angles is the perpendicular distance between the two parallel lines

To prove that two lines are perpendicular, one of the following theorems must be true:

• If two lines are perpendicular to each other, then they form four right angles.
  

If m ⊥ n, then we can conclude that ∠1, ∠2, ∠3

and ∠4 are right angles.

• If the angles in a linear pair are congruent, then the lines containing their sides are perpendicular.
  

If ∠1 and ∠2 form a linear pair and ∠1 ≅ ∠2, then l1 ⊥ l2.

• If two angles are adjacent and complementary, the non-common sides are perpendicular.
  

If ∠1 and ∠2 form a linear pair and ∠1 ≅ ∠2, then l1 ⊥ l2.

∠CAR and ∠EAR are complementary and adjacent, then AC ⊥ AE.

Proving Theorems on Perpendicular Lines

1. If two lines are perpendicular, then they form four right angles.
2. If the angles in a linear pair are congruent, then the lines containing their sides are perpendicular.
3. In a plane, through a point on a given line there is one and only one line perpendicular to the given line.
4. In a plane, a segment has a unique perpendicular bisector.
5. If two angles are adjacent and complementary, the non-common sides are perpendicular.

 

The following video will explain how to construct a perpendicular line to a point and a perpendicular line through a point not on a line.

Constructing Perpendicular Lines

Criteria of perpendicularity of straight line and plane:

1)  If a straight line is perpendicular to two interesting straight lines, lying in a plane,  

     then it is perpendicular to this plane.

2)  If a plane is perpendicular to one of parallel straight lines, then it is perpendicular  

     to the other.

Theorem about three perpendiculars. A straight line, that lies in a plane and is perpendicular to a projection of straight line inclined to this plane, is perpendicular to this straight line inclined to plane.

Theorem about common perpendicular to two crossing straight lines.  Any two crossing straight lines have the only common perpendicular.

 KINDS OF QUADRILATERALS

Quadrilateral is a polygon with four sides. Quadrilaterals are classified as follows:

1. Trapezium – a quadrilateral with no pair of parallel sides.
   

   

   Trapezium

   
   

   
   
2. Trapezoid – a quadrilateral with exactly one pair of parallel sides. If the non-parallel sides are congruent, the trapezoid is said to be isosceles.
   

   

   Trapezoid

   
   

   
   
3. Parallelogram – a quadrilateral with two pairs of parallel and congruent sides. There are two special kinds of parallelogram: the rectangle which has four right angles and the rhombus which has four congruent sides. A square which has four congruent angles and four congruent sides can be a rectangle or a rhombus because it satisfies the definition for a rectangle and a rhombus.
   

   

   Parallelogram

 

Conditions to Prove that a Quadrilateral is a Parallelogram

Given a parallelogram, related definition and theorems are stated as follows:

1. A parallelogram is a quadrilateral with both pairs of opposite sides parallel.
2. If a quadrilateral is a parallelogram, then 2 pairs of opposite sides are congruent.
3. If a quadrilateral is a parallelogram, then 2 pairs of opposite angles are congruent.
4. If a quadrilateral is a parallelogram, then the consecutive angles are supplementary.
5. If a quadrilateral is a parallelogram, then the diagonals bisect each other.
6. If a quadrilateral is a parallelogram, then the diagonals form two congruent triangles.

 To prove a parallelogram, related definition and theorems are stated as follows:

(Many of these theorems are converses of the previous theorems.)

1. A parallelogram is a quadrilateral with both pairs of opposite sides parallel.
2. If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
3. If both pairs of opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram.
4. If one angle is supplementary to both consecutive angles in a quadrilateral, then the quadrilateral is a parallelogram.
5. If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a  parallelogram.
6. If one pair of opposite sides of a quadrilateral are both parallel and congruent, then the quadrilateral is a parallelogram.

To have more understanding of the properties of a parallelogram, you may visit the following link:

https://www.youtube.com/watch?feature=player_detailpage&v=0rNjGNI1Uzo

TRIANGLE INEQUALITIES

Have you ever wondered how artists utilize triangles in their artworks? Have you ever asked yourself how contractors, architects, and engineers make use of triangular features in their designs? What mathematical concepts justify all the triangular intricacies of their designs?

The following terms, theories and postulates will give you a better understanding of this topic.

Axioms of Equality

• Reflexive Property of Equality - for all real numbers p, p = p.
• Symmetric Property of Equality - for all real numbers p and q, if p = q, then q = p.
• Transitive Property of Equality - for all real numbers p, q, and r, if p = q and q = r, then p = r.
• Substitution Property of Equality - for all real numbers p and q, if p = q, then q can be substituted for p in any expression.

Properties of Equality

• Addition Property of Equality - for all real numbers p, q, and r, if p = q, then p + r = q + r.
• Multiplication Property of Equality - for all real numbers p, q, and r, if p = q, then pr = qr.

Definitions, Postulates and Theorems on Points, Lines, Angles and Angle Pairs

• Definition of a Midpoint - if points P, Q, and R are collinear (P–Q–R) and Q is the midpoint of PR,then PQ ≅ QR.
• Definition of an Angle Bisector - if QS bisects ∠PQR, then ∠PQS ≅ ∠SQR.
• Segment Addition Postulate - if points P, Q, and R are collinear (P–Q–R) and Q is between points P and R, then PQ + QR ≅ PR.
• Angle Addition Postulate - if point S lies in the interior of ∠PQR, then ∠PQS + ∠SQR ≅ ∠PQR.
• Definition of Supplementary Angles - two angles are supplementary if the sum of their measures is 180º.
• Definition of Complementary Angles - two angles are complementary if the sum of their measures is 90º.
• Definition of Linear Pair - linear pair is a pair of adjacent angles formed by two intersecting lines
• Linear Pair Theorem - if two angles form a linear pair, then they are supplementary.
• Definition of Vertical Angles - vertical angles refer to two non-adjacent angles formed by two intersecting lines.
• Vertical Angles Theorem - vertical angles are congruent.

How to Measure Angles Using a Protractor

To master the skill in estimating the measures of angles, you can visit the following links:

     Interactive:

             Angle Measures

     Games:

            Angles

            Angles Game

            Kung Fu Angles

            Banana Hunt

            Fruit Picker

To measure an angle, the protractor’s origin is placed over the vertex of an angle and the base line along the left or right side of the angle. The illustrations below show how the angles or angles of a triangle are measured using a protractor.

Definitions and Theorems on Triangles

• The sum of the measures of the angles of a triangle is 180º.
• Definition of Equilateral Triangle - An equilateral triangle has three sides congruent.
• Definition of Isosceles Triangle - 
  An isosceles triangle has two congruent sides; 
  Base angles of isosceles triangles are congruent; 
  Legs of isosceles triangles are congruent.
• Exterior Angle of a Triangle - An exterior angle of a triangle is an angle that forms a linear pair with an interior angle of a triangle when a side of the triangle is extended.
• Exterior Angle Theorem - The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles of the triangle.
• Sides and Angles of a Triangle
  
  
  

Definition and Postulates on Triangle Congruence

• Definition of Congruent Triangles: Corresponding parts of congruent triangles are congruent (CPCTC).

Figure 1

• Included Angle (Figure 1)

                 Included angle is the angle formed by two distinct sides

                 of a triangle.

                        • ∠YES is the included angle of EY and ES

                        • ∠EYS is the included angle of YE and YS

                        • ∠S is the included angle of SE and SY

Figure 2

• Included Side (Figure 2)

                 Included side is the side common to two angles of a

                 triangle.

                        • AW is the included side of ∠WAE and ∠EWA

                        • EW is the included side of ∠AEW and ∠AWE

                        • AE is the included side of ∠WAE and ∠AEW

• SSS Triangle Congruence Postulate. If  three sides of one triangle are congruent respectively to three sides of another triangle, then the two triangles are congruent.
• SAS Triangle Congruence Postulate. If two sides and the included angle of one triangle are congruent respectively to two sides and the included angle of another triangle, then the two triangles are congruent.
• ASA Triangle Congruence Postulate. If two angles and the included side of one triangle are congruent respectively to two angles and the included side of another triangle, then the two triangles are congruent.

The following links could help you master the Triangle Congruence Postulates:

               Congruent Triangles

               Congruent Triangles 2

        

Properties of Inequality

• For all real numbers p and q where p > 0, q > 0:

             • If p > q, then q < p.
             • If p < q, then q > p.

• For all real numbers p, q, r and s, if p > q and r ≥ s, then p + r > q + s.
• For all real numbers p, q and r, if p > q and r > 0, then pr > qr.
• For all real numbers p, q and r, if p > q and q > r, then p > r.
• For all real numbers p, q and r, if p = q + r, and r > 0, then p > q.

  

  The last property of inequality is used in geometry as illustrated above

                                              a. Q is between P and R

                                              b. ∠1 and ∠2 are adjacent angles

                           a.) PR ≅ PQ + QR, then PR > PQ and PR > QR.

                   b.) ∠PQR ≅ ∠1 + ∠2, then m∠PQR > m∠1 and m∠PQR > m∠2

Theorem 1:

The sum of the lengths of any two sides of a triangle must be greater than the third side.

Example

Suppose we know the lengths of two sides of a triangle, and we want to find the "possible" lengths of the third side.

According to our theorem, the following 3 statements must be true:
5 + x > 9    So, x > 4	5 + 9 > x     So, 14 > x	x + 9 > 5 So, x > -4  (no real information is gained here since the lengths of the sides must be positive.)

Putting these statements together, we get that x must be greater than 4, but less than 14.  So any number in the range 4 < x < 14 can represent the length of the missing side of our triangle.

Theorem 2: also ...	In a triangle, the longest side is across from the largest angle.
Theorem 3:	In a triangle, the largest angle is across from the longest side.

                              

Since 100° is the largest angle in this triangle,             Since AB, which is 7, is the longest side,

  across from it is the longest side, AB                         across from it is the largest angle, angle C

These theorems can be modified to apply to a discussion of only two angles within the triangle:

Theorem:  In a triangle, the longer side is across from the larger angle.
Theorem:  In a triangle, the larger angle is across from the longer side.

Example

Suppose we want to know which side of this triangle is the longest.

Before we can utilize our theorem, we need to know the size of <B.  We know that the 3 angles of the triangle add up to 180°.	80 + 40 + x = 180            120 + x = 180                      x = 60
We have now found that <B measures 60°.  According to our theorem, the longest side will be across from the largest angle.	Now that we know the measures of all 3 angles, we can tell that <A is the largest. This means the side across from <A is the longest side.

Theorem 4:

The measure of the exterior angle of a triangle is greater than the measure of either nonadjacent interior angle.

THE BLOGGERS ♥

This portion gives some basic information about the creators of this page. Their individual reflections regarding Educational Technology and the making of this requirement are also stated here.

    

Name: Juliemer B. Absalon

Birthday: January 08, 1996

Address: Zone 10A Blk. 8 Brgy. Fatima, General Santos City

Email: jbabsalon@yahoo.com

Year & Course: 3rd year - BSED Mathematics

             

            I’m glad that technology-related subjects, like our Educational Technology, are offered to students taking-up education courses. Being exposed to technology integration in teaching will be very helpful and useful for us, as future educators. By creating sites and presenting certain topics and corresponding discussions, including examples and interactive stuffs in it, will be very convenient for both the teacher and students.

            I’m very grateful that we had been given the task to create our own blog site. At first, I was a bit hesitant if we can do it and come up with this kind of page, since I haven’t tried making this before. In the process of doing this blog site, I realized that creating even a simple one will require a lot of time, effort and especially, cooperation from your group mates.

            I've really learned a lot from this project, not just creating and publishing pages, but most importantly, how working hand-in-hand and dealing with problems together will result to desired goals. I am proud to say that this blog is the outcome of our individual dedication and oneness as a group.

- Juliemer ♥

Name: Arianne Grace B. Costales

Birthday: January 27, 1996

Address: Zone 2 Blk 5 Brgy. Fatima, General Santos City

Email: costalesarianne@gmail.com
Year & Course: 3rd year -  BSED Mathematics

We all know that Educational Technology is the study and ethical practice of facilitating learning and improving performance by creating, using and managing appropriate technological processes and resources. This subject is such a big help not only for us future teachers but also to our students.

I thought making or creating a blog is just easy. But it’s not. It requires a lot of effort in order to have a creative output. My groupmates and I had a very hard time building this blog. Not because we want it to be beautiful but because we don’t have any background at blogging at all! But I am very happy that we tried our best and come up with this output. This will be a big help to students and other researchers who are finding answers to their questions about parallelism, perpendicularity and inequalities of a triangle.

- Arianne Grace ♥

            

Name: Monhannah Ramadeah C. Limbutungan

Birthday: January 11, 1997

Address: Ladies Dorm, MSU-GSC

Email: mlimbutungan@yahoo.com

Year & Course: 3rd year -  BSED Mathematics

Educational technology is the use of technology to improve education.  One example of integrating technology in education is through making weblog or our own website. It just so happened that our teacher gave as the task of making our own weblog/ website.
    

I got so excited and a bit nervous since it when I heard about it. I was just like “Shet. Gagawa tayo sarili natin blogsite? Grabe lang talaga. Parang mahirap man gawin” I am just so glad that one of our group mates did know atleast how to create our own blog site. It was really fun making it. We did a lot of exploration just to make our blog look nice and well-designed. In making our blog site, we did a lot of effort to come up with this outcome. I’m just so proud of ourselves since we are able to make our own blog site.

- Monhannah Ramadeah ♥

             

Name: Gebrielle Rica L.Aguinaldo

Birthday: September 26, 1995

Address: Polomolok, South Cotabato

Email: gabyluderico@yahoo.com

Year & Course: 3rd year - BSED Mathematics

When I was enrolled in the subject Educational Technology, I was confused on how to relate technology and mathematics. There are times that I was wondering about the positive and negative effects of the technology to both teachers and students. Teachers use media in teaching and as what I have observed, as a student, I become more active in listening and participating in our lessons.

As we had this seminar about web blogging, I learned about on how to create an account. And as we had given the chance to make our own web blog based on the different topics that has been given to us, I learned how to explore things, especially on animation and the creative designs that can be used in the web blog.

- Gebrielle Rica ♥

Name: Errolha Lynn T. Seballos

Birthday: September 14, 1995

Address: Zone 2 Blk 6 Brgy. Fatima, General Santos City

Email: wiiisheart@yahoo.com

Year & Course: 3rd year - BSED Mathematics

I like technology to be honest because I’m using technology every day. So when I heard about the subject Educational Technology I was really interested about the subject because I know that we will be engaging with technologies and other programs of it. And I know that somehow I won’t be having difficulties since I've experienced a lot when it comes to technology. So when I knew that EdTech was not really all about technology it’s something more than that. We do not just use technology for email purposes or conferences we also use technology as our guide in the different lessons that we will be encountering.

I've learned that blogs and websites are not just for entertainment, they have something beyond that, like educational and business purposes. There is also that innovative way in teaching different subjects in technology, like in English technology can facilitate learning and it would be a great help for the learners to learn English easier since it has an audio that can teach them and the videos and pictures as well.

- Errolha Lynn ♥

Name: Ever Joy P. Hinampas

Birthday: June 17, 1995

Address: Brgy. Tinagakan, General Santos City

Email: everjoyhinampas@yahoo.com

Year & Course: 3rd year - BSED Mathematics

As I am enrolled in EdTech, I learned so many things about technologies especially as to how to apply it in teaching. I found our lessons very interesting because I know within myself that I am not that much knowledgeable when it comes to technologies. As our discussions continue, I know that I have gained new information and tips which I think would be useful to my future profession.

In every subject, I believe that there is a requirement needed in order to pass. It happened that making our own web blog site is the requirement for this subject. At first, I was a little bit nervous knowing that I have no experience in making a web blog. I cannot even remember that I visited any web blog site in my entire life. So believe that this whole thing is new to me.

I am so glad that my group mates have some knowledge about making a web blog. At first, I have no idea with what they are doing. But as they seek for my help, I was kind of hesitant because I am afraid that instead of helping them, I might do something terrible which my damage or web blog. As a team, they encouraged and assured me that they will guide me with this.

So I decide to help and I was assigned to do the typing. I was surprised that I found myself having fun and enjoying the task given to me. It was so hilarious and I was ashamed of myself at first for I do not even know how to operate some things but they guided me that’s why I finally accomplished my work. I have so much fun working with my team and I realized that someone could actually learn while enjoying.

I can say that I am proud of our web blog for it is the fruit of our labor and hardwork. I gained so much learning not just on how to make a web blog but also some important lessons like it is much easier to do and accomplish a task when there is cooperation and teamwork. With these, I am happy to know that we succeeded in our web blog.

- Ever Joy ♥

We hope that our blog had given you additional knowledge about Parallelism & Perpendicularity and Triangle Inequalities.